本試卷總分100分，考試時間150分鐘。

一、單項選擇題（1—20每小題1分，21—30每小題2分， 共40分）

1.函數y=xsinx在其定義域內是（　　　）

A.有界函數
B.周期函數
C.無界函數
D.奇函數

2.函數的定義域是（　　　）

A.[-1,0)∪(0,1]
B.[-1,0)
C.(-∞,-1]∪[1,∞)
D.(0,1]

3.函數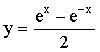是（　　　）

A.偶函數
B.奇函數
C.非奇非偶函數
D.周期函數

4.設|q|<1，則=（　　　）

A.不存在
B.-1
C.0
D.1

5.若函數f(x)在點x0處可導且，則曲線y=f(x)在點（x0, f(x0)）處的法線的斜率等于（　　　）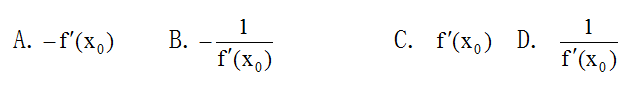

A.
B.
C.
D.

7.設y=a0+a1x+a2x^2+a3x^3，則y'''=（　　　）

A.
B.
C.
D.

8.設，則（　　　）

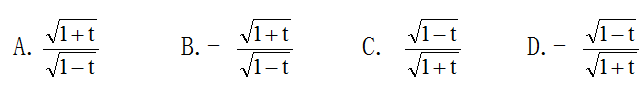
A.
B.
C.
D.

9.函數f(x)=arctgx在[0，1]上使拉格朗日中值定理結論成立的c是（　　　）

A.
B.
C.
D.

10.函數y=x+tgx在其定義域內（　　　）

A.有界
B.單調減
C.不可導
D.單調增

12.=（　　　）

A.
B.
C.
D.

16.二元函數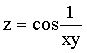的所有間斷點是（　　　）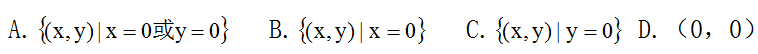

A.
B.
C.
D.

15.方程組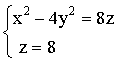在空間表示（　　　）

A.雙曲柱面
B.（0，0，0）
C.平面z=8上的雙曲線
D.橢圓

20.等比級數a+aq+aq^2+…+aq^(n-1)+…(a≠0)（　　　）

A.當|q|<1時發散；當|q|≥1時收斂
B.當|q|≤1時發散；當|q|>1時收斂
C.當|q|≤1時收斂；當|q|>1時發散
D.當|q|<1時收斂；當|q|≥1時發散

21.（　　　）

A.2
B.1
C.0
D.不存在

25.函數y=xe^-x的單調增區間是（　　　）

A.（-∞,+ ∞）
B.[1,+∞)
C.（-∞,1]
D.(1,+∞)

26.過兩點P1(1,1,1),P2(2,3,4)的直線方程為（　　　）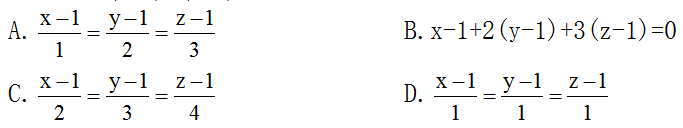

A.
B.
C.
D.

29.29．微分方程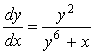是（　　　）

A.一階線性齊次方程
B.一階線性非齊次方程
C.二階線性微分方程
D.六階線性微分方程

6.設y=x^4+ln3，則y'=（　　　）

A.
B.
C.
D.

11.函數的圖形的水平漸近線方程為（　　　）

A.y=1
B.x=1
C.y=0
D.x=0

13.設，則=（　　　）

A.sinx
B.-sinx
C.cosx
D.-cosx

18.設（σ）是矩形域：a≤x≤b,c≤y≤d，則=（　　　）

A.a+b+c+d
B.abcd
C.(b-a)(d-c)
D.(a-b)(d-c)

27.微分方程y"+y=0的通解為（　　　）

A.y=sinx+cosx
B.y=cosx
C.y=sinx
D.y=C1cosx+C2sinx

30.當|x|<1時，冪級數1+x+x^2+…+x^n+…收斂于（　　　）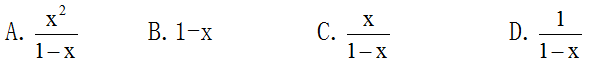

A.
B.
C.
D.

17.設，則=（　　　）

A.4
B.2
C.1
D.1/2

19.微分方程x(y')^2-2yy'+x=0是（　　　）

A.二階微分方程
B.一階微分方程
C.二階線性微分方程
D.可分離變量的微分方程

28.級數（　　　）

A.發散
B.絕對收斂
C.條件收斂
D.斂散性不能確定

24.（　　　）

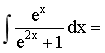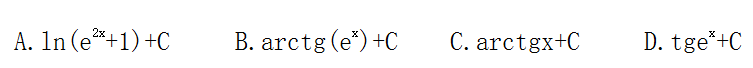
A.
B.
C.
D.

14.廣義積分（　　　）

A.收斂
B.斂散性不能確定
C.收斂于-2
D.發散

22.（　　　）

A.e^-1
B.e
C.+∞
D.1

23.設函數f(x)=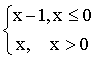,則f(x)在x=0是（　　　）

A.可微的
B.可導的
C.連續的
D.不連續的

二、計算題（每小題6分，共42分）

1.求.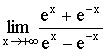          

3.求.            

6.求二重積分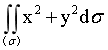其中σ：1≤x^2+y^2≤2.

7.判別級數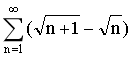的斂散性.

2.設y=x^x(x>0)，求y'.

5.求微分方程sinxcosydx=cosxsinydy滿足初始條件y|x=0=的特解.

4.求.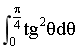

三、應用和證明題（每小題6分，共18分）

1.求由拋物線y^2=4ax(a>0)及直線x=x0(x0>0)所圍成的平面圖形繞x軸旋轉而成的旋轉體的體積.

2.求函數f(x)=的極值.

3.設z=, 其中F(u)為可導函數, 求證.